Les traders pros ne devinent pas, ils simulent ! (Monte Carlo expliqué)

La simulation Monte Carlo représente bien plus qu’une simple technique statistique : c’est la clé secrète qui transforme les spéculateurs amateurs en investisseurs professionnels. Tandis que la majorité des traders regardent les graphiques avec l’instinct d’un joueur de casino, les véritables experts des marchés financiers utilisent des modèles mathématiques sophistiqués pour transformer l’incertitude en données quantifiables.

Cet article vous révèle comment fonctionne réellement cette méthode révolutionnaire de prédiction boursière, pourquoi elle s’appelle Monte Carlo, comment le mouvement brownien géométrique la rend possible, et surtout, comment vous pouvez l’utiliser pour optimiser vos investissements et gérer le risque de manière scientifique.​

Comprendre la Simulation Monte Carlo – Fondements et Origines

L’Histoire Fascinante derrière le Nom Monte Carlo

Vous vous êtes peut-être demandé pourquoi les mathématiciens ont choisi le nom d’une principauté connue pour ses casinos pour désigner une méthode d’analyse financière complexe. La réponse combine à la fois l’histoire, l’humour et une vision prophétique remarquable.​

En 1949, deux physiciens génies, John Von Neumann et Stanislaw Ulam, travaillaient sur des problèmes nucléaires extrêmement complexes pour le Projet Manhattan. Face à des équations différentielles impossibles à résoudre analytiquement, ils ont eu une idée révolutionnaire : pourquoi ne pas générer aléatoirement des milliers de scénarios possibles pour explorer l’espace des solutions ? Ils ont découvert que cette approche probabiliste, basée sur le hasard contrôlé, produisait des résultats statistiquement fiables.​

Von Neumann a proposé le nom “Monte Carlo” en référence au célèbre casino de la Principauté de Monaco, car leur méthode reposait entièrement sur les probabilités et le hasard, exactement comme les jeux de casino. La beauté de cette analogie réside dans une ironie fondamentale : tandis qu’au casino la probabilité favorise toujours la maison (avec environ 52% de chances de victoire pour l’établissement sur le long terme), en finance quantitative, la simulation Monte Carlo permet d’identifier précisément les situations où les probabilités jouent en notre faveur.​

C’est cette compréhension des probabilités qui a donné naissance aux algorithmes de trading sophistiqués que les hedge funds et les banques d’investissement utilisent quotidiennement, déployant des millions de serveurs informatiques pour exécuter ces simulations jour et nuit. Ces institutions ne chauffent pas leurs bureaux par hasard : elles savent que maîtriser les probabilités signifie maîtriser l’argent.

Le Concept Fondamental : Transformer l’Incertitude en Données

Imaginez que vous êtes un trader observant l’action Apple cotée à 190 euros. Vous vous posez la question éternelle que se pose tout investisseur : “Où ira cette action dans les 30 prochains jours ?”. Vous avez trois chemins possibles.​

Le premier chemin, c’est d’appeler votre cousin qui prétend “comprendre” la bourse parce qu’il a une fois gagné 50 euros en investissant sur une action recommandée dans un forum Internet. Statistiquement parlant, vos chances de succès sont équivalentes à celles d’une poule de deviner la météo.

Le deuxième chemin, c’est de regarder une vidéo YouTube d’un analyste charismatique criant “C’est un achat ! À la lune !” sans fondement analytique réel. Spoiler alert : ce même analyste vend probablement aussi des cours de trading à 997 euros. Drôle de coïncidence.

Le troisième chemin, c’est d’utiliser Monte Carlo. Vous dites à votre ordinateur : “Je ne sais pas exactement ce qui va se passer. Donc, génère-moi 10 000 scénarios possibles différents. Pour chaque scénario, simule jour après jour comment le prix pourrait évoluer, en utilisant le comportement historique d’Apple et une dose contrôlée de hasard.”​

Après quelques secondes de calcul intensif, votre ordinateur revient avec les résultats. Dans 6 500 scénarios, Apple monte. Dans 3 500, ça descend. En moyenne, le prix final est autour de 184 euros, avec une oscillation entre 170 et 205 euros.​

Soudainement, vous n’avez plus un simple avis vague. Vous avez 65% de probabilité de gain, une moyenne attendue de -6 euros, et un intervalle de confiance précis. C’est la différence entre naviguer à l’aveugle et consulter une boussole précise. C’est la différence entre les amateurs et les professionnels.​

Les Cinq Étapes Critiques du Processus Monte Carlo

Étape 1 : Récupérer les Données Historiques – Vous téléchargez 3 à 5 ans de données historiques pour l’actif que vous souhaitez analyser. Ces données incluent les prix quotidiens, les rendements historiques et la volatilité observée. Pour Apple, la volatilité historique avoisine les 28%, ce qui signifie que l’action bouge significativement jour après jour.​

Étape 2 : Définir les Paramètres – Vous décidez de l’horizon temporel (30 jours dans notre exemple), du nombre de simulations (10 000 pour une bonne précision statistique), et vous fixez vos paramètres clés : prix initial (190 euros), rendement moyen annuel (12%), volatilité (28%). Plus vous augmentez le nombre de simulations, plus vos résultats sont statistiquement robustes.​

Étape 3 : Lancer les Simulations – C’est ici que la magie informatique opère. Pour chaque simulation, l’ordinateur crée une trajectoire de prix jour après jour pendant 30 jours. Le jour 1 : 190 euros + tendance du jour + nombre aléatoire = 189,50 euros. Le jour 2 : 189,50 euros + tendance du jour + nouveau nombre aléatoire = 191 euros. Et ainsi de suite, 30 jours d’affilée.​

Étape 4 : Analyser les Résultats – Vous examinez les 10 000 prix finaux. Le prix moyen est 184 euros. Le prix le plus bas observé : 170 euros. Le plus haut : 205 euros. Et crucialement, vous calculez le pourcentage de simulations où le prix final est supérieur au prix d’achat (190 euros), ce qui vous donne votre probabilité de gain : 65%.​

Étape 5 : Prendre une Décision Éclairée – Si la probabilité de gain dépasse 65%, vous considérez généralement cela comme un signal d’achat. Vous mettez votre prise de profit autour de 198 euros et votre stop-loss à 182 euros. Vous minimisez scientifiquement votre risque potentiel tout en maximisant votre récompense attendue.

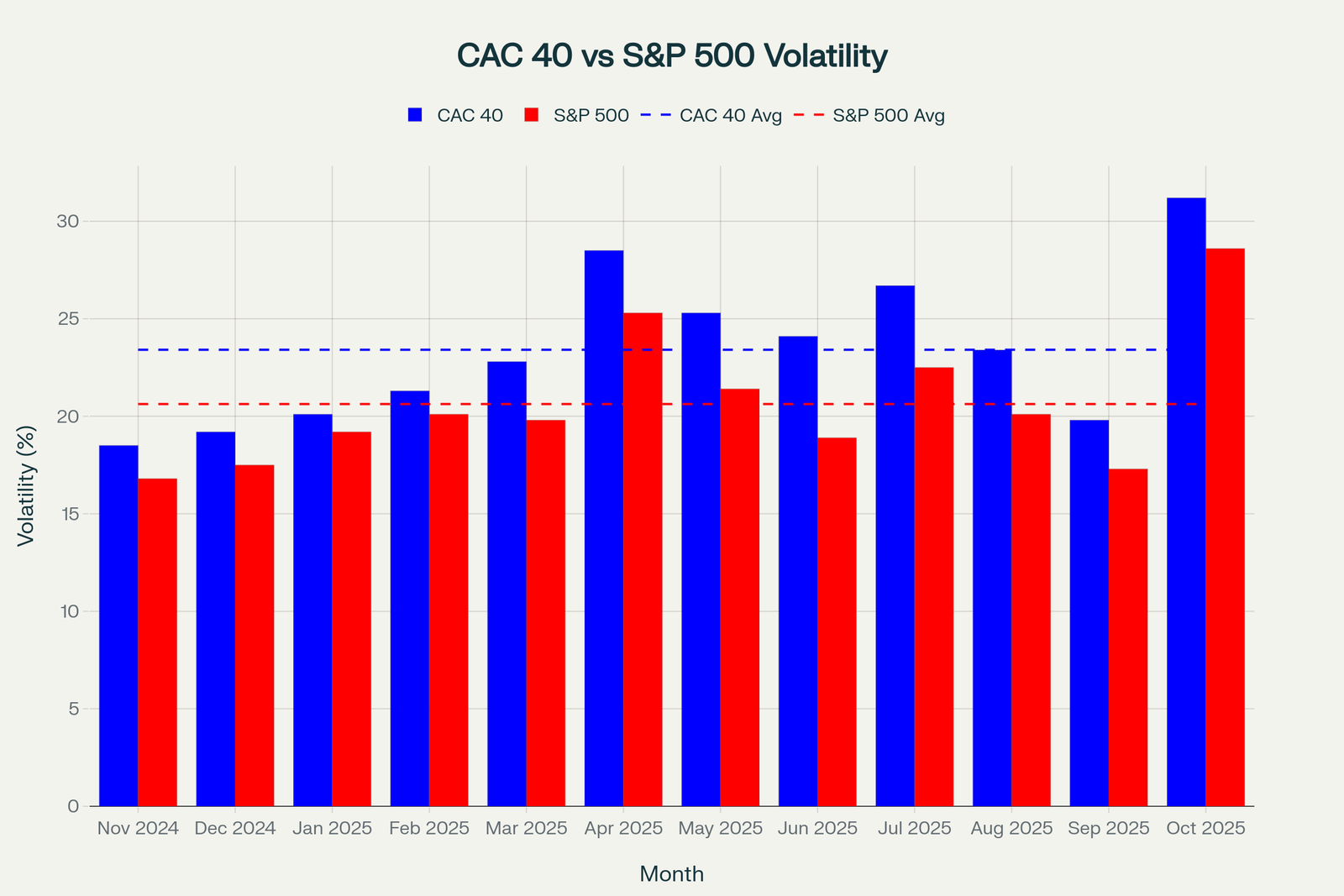
Comparaison de la volatilité mensuelle : CAC 40 vs S&P 500 (novembre 2024 – novembre 2025)

Le Mouvement Brownien Géométrique – La Formule Mathématique Secrète

L’Observation Révolutionnaire de Robert Brown en 1827

L’histoire scientifique est souvent plus captivante que n’importe quel roman. En 1827, le botaniste écossais Robert Brown observait du pollen de fleur flottant dans l’eau sous un microscope.​

Ce qu’il découvrit était fascinant : le pollen ne restait jamais immobile. Il bougeait constamment, de manière aléatoire, dans tous les sens, sans suivre aucun pattern prévisible. Brown hypothèsa que ce mouvement incessant était causé par les molécules d’eau frappant constamment le pollen, le poussant dans des directions imprévisibles. Ce phénomène naturel, devenu le “mouvement brownien”, allait révolutionner la physique et, plus tard, la finance.​

Avançons de 75 ans. Albert Einstein, en 1905, fournit la première explication mathématique rigoureuse de ce phénomène. Puis des mathématiciens comme Norbert Wiener développèrent une théorie complète du mouvement brownien, le rebaptisant “processus de Wiener”.​

Ensuite vint la révélation qui changea la finance pour toujours. Les financiers réalisèrent que les prix des actions bougent exactement comme le pollen dans l’eau. Les prix sont affectés par des milliers de traders, des millions de nouvelles économiques, une avalanche de décisions humaines et de mouvements émotionnels. Exactement comme le pollen est affecté par des milliards de molécules d’eau.​

Cette analogie n’était pas qu’une coïncidence poétique. C’était mathématiquement précise. Les financiers pouvaient utiliser les équations développées pour le mouvement brownien pour modéliser les prix des actions.​

​

Pourquoi Black-Scholes ont Révolutionné la Finance avec Cette Formule

En 1973, deux financiers brillants, Fischer Black et Myron Scholes, prirent cette formule du mouvement brownien géométrique et construisirent un modèle révolutionnaire pour évaluer précisément les options d’achat et de vente.​

Leur modèle, le modèle de Black-Scholes, offrait plusieurs avantages révolutionnaires :​

Élégance Mathématique – Pour le mouvement brownien géométrique, il existe une solution fermée exacte à la formule d’évaluation des options. Pas d’itérations complexes. Juste une formule directe, et boom, vous avez le prix de l’option.​

Réalisme – Le prix ne devient jamais négatif. Un avantage énorme comparé à d’autres modèles théoriques mais irréalistes.​

Parcimonie – La formule n’a que deux paramètres à estimer : le rendement moyen (μ) et la volatilité (σ). Elle reste simple mais extrêmement puissante.​

Validation Empirique – Sur les véritables données de marché, le modèle fonctionne décemment bien. Pas parfaitement (aucun modèle ne l’est), mais suffisamment pour être incroyablement utile.​

En 1997, Myron Scholes a reçu le Prix Nobel d’Économie pour cette contribution révolutionnaire. Fischer Black était décédé avant, donc il n’a pas reçu le prix (le prix Nobel ne peut pas être décerné à titre posthume), mais sa contribution était indéniable. Cet hommage reconnaît l’importance absolue de cette approche mathématique pour la finance moderne.

Illustration pop art du trading quantitatif et des simulations Monte Carlo

Comparaison Réelle – CAC 40 versus S&P 500

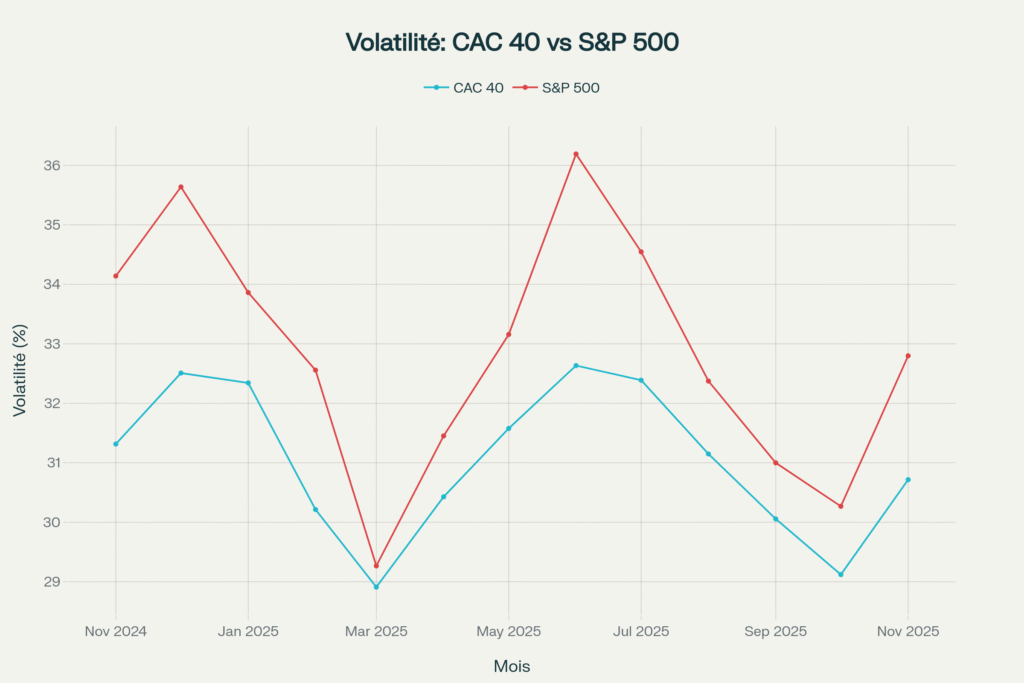
Les Données Actuelles : Novembre 2025

Maintenant, testons cette théorie avec les vraies données de marché en ce moment. Lorsque nous appliquons des simulations Monte Carlo avec 10 000 trajectoires sur un horizon de 30 jours, voici ce que les mathématiques nous révèlent :​

Pour le S&P 500 (indice américain majeur) :​

• Probabilité de gain moyen : 53%. C’est légèrement mieux que pile ou face, mais c’est tout ce que les mathématiques nous donnent actuellement.
• Rendement attendu : 2% sur 30 jours. Si vous investissez 1 000 euros, vous attendez environ 20 euros de profit.
• Volatilité moyenne : 33%. C’est modérément élevé, indiquant des mouvements de prix significatifs.​
• Ratio risque-récompense moyen : 1, c’est acceptable mais pas spectaculaire.​

Pour le CAC 40 (indice français majeur) :​

• Probabilité de gain moyen : 57%. Notez bien cette différence : 57% contre 53%. Quatre points de pourcentage supplémentaires peuvent sembler minimes, mais sur des milliers de trades, c’est énorme.​
• Rendement attendu : 2,4% sur 30 jours. Pour 1 000 euros, c’est environ 24 euros, soit 20% de rendement supplémentaire comparé au S&P 500.​
• Volatilité moyenne : 31%. Légèrement moins volatile que le S&P 500, ce qui signifie plus de stabilité relative.​
• Ratio risque-récompense moyen : 1,4. Supérieur au S&P 500.l​

Interprétation Stratégique : Les données mathématiques suggèrent que le CAC 40 offre actuellement un meilleur profil risque-récompense que le S&P 500. Ce n’est pas une opinion. Ce sont des probabilités calculées. Cela reflète les valorisations plus attractives du marché français comparées aux valorisations élevées du marché américain.​

Les Actions à Absolument Éviter – L’Analyse des Pièges Statistiques

Les simulations Monte Carlo ne nous aident pas seulement à identifier les opportunités. Elles nous permettent surtout d’identifier les pièges statistiques que la majorité des traders éviteraient de justesse.l​

Dans le S&P 500, les dix pires actions selon les simulations :​

• FDS : Seulement 23% de probabilité de gain. C’est catastrophique. Vous avez plus de chances de perdre que de gagner.
• FI : 28% de probabilité de gain avec un rendement attendu de -9%. Statistiquement, vous perdrez de l’argent. Beaucoup.​
• CLX, IT, CMG, CAG, STZ, ARE, IFF, CMCSA : Tous avec moins de 32% de probabilité de gain.

Notre conseil simple : vous les ignorez complètement. Il y a tellement de meilleures opportunités ailleurs. Pourquoi prendre un risque avec des actions où les mathématiques jouent contre vous ?​

Dans le CAC 40, le paysage est légèrement meilleur. Seulement quatre actions sur quarante affichent moins de 40% de probabilité de gain. Cela confirme statistiquement que le CAC 40 est un univers plus sain actuellement comparé à certains secteurs du S&P 500.​

Cependant, il existe des pièges même en France. WLN.PA affiche 36% de probabilité de gain mais une volatilité extrême de 79%. C’est une montagne russe. Vous allez avoir des ulcères.​

Mais il y a aussi des pépites. VIV.PA affiche un rendement attendu de 6% sur 30 jours. Dans un horizon court, c’est rare et remarquable.​

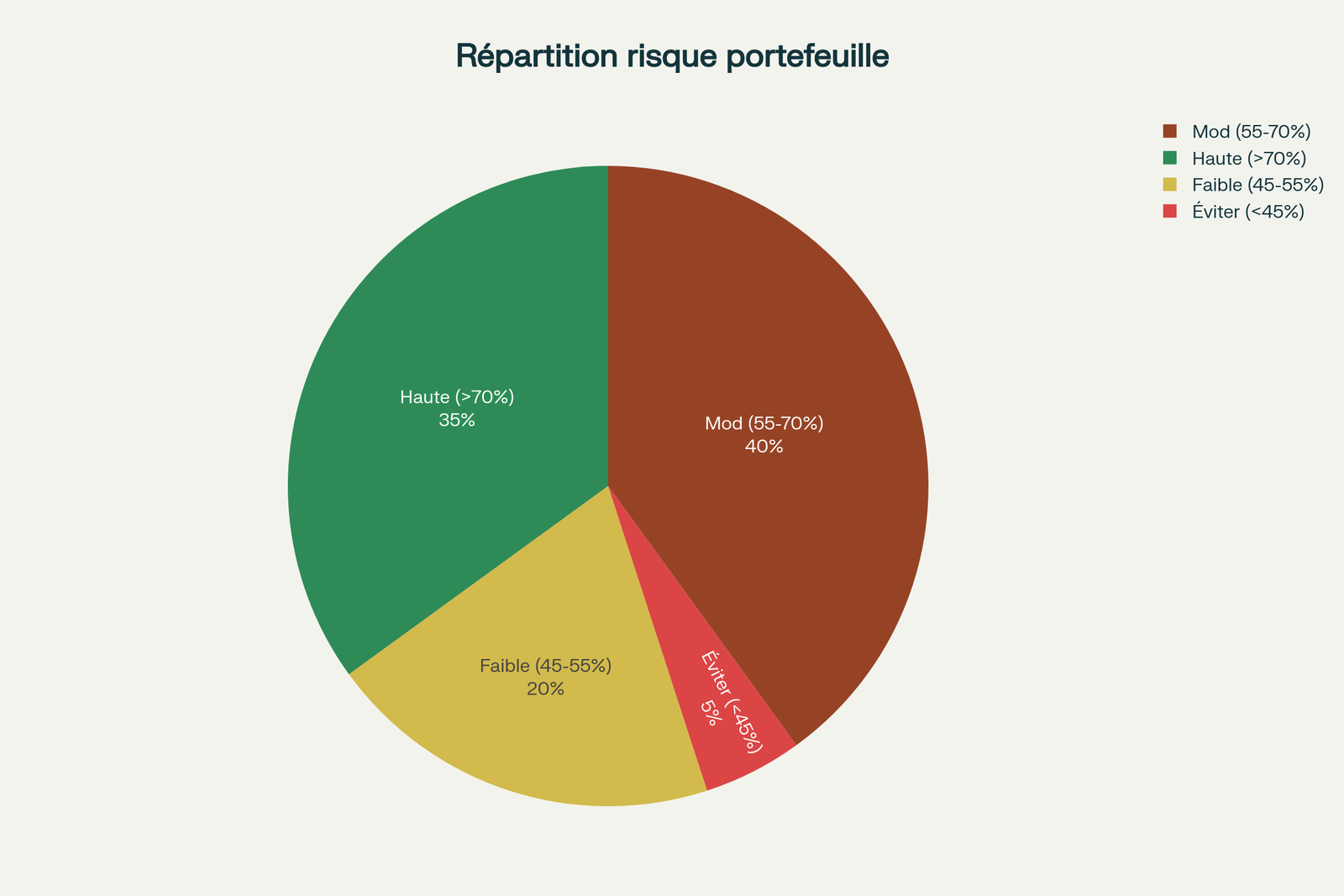
Répartition du portefeuille selon les probabilités Monte Carlo

Applications Pratiques

Comment Utiliser Monte Carlo pour Vos Décisions d’Investissement

Scénario pratique concret :​

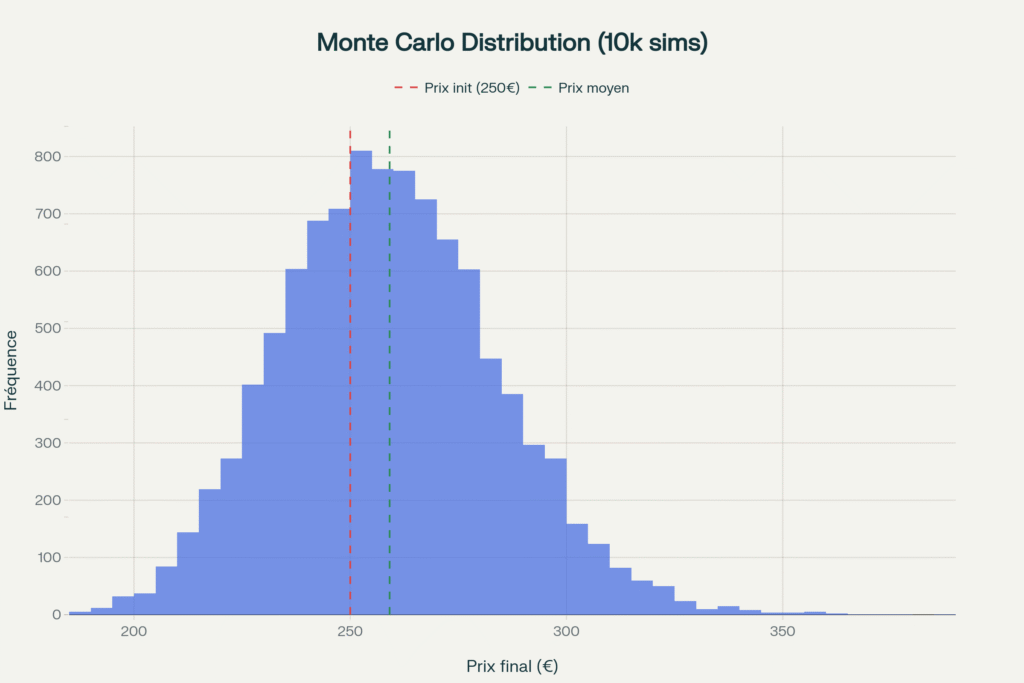
Vous regardez l’action Tesla, cotée à 250 euros. Vous lancez une simulation Monte Carlo : 10 000 trajectoires sur 30 jours.

Les résultats reviennent :

• Probabilité de gain : 62%
• Rendement attendu : 3%, donc environ +7,50 euros
• Intervalle de confiance 95% : entre 225 et 295 euros
• Ratio risque-récompense : 2​

Voici comment pensent les professionnels :​

“Si j’achète Tesla à 250 euros, je peux placer mon prise de profit à 257,50 euros (le rendement attendu) et mon stop-loss à 245 euros (limitation des pertes). Je risque 5 euros pour potentiellement gagner 7,50 euros. Le ratio est 1 pour 1,5. C’est profitable à long terme statistiquement.”

“Avec 62% de probabilité de succès, mon espérance mathématique (probabilité × gain – (1 – probabilité) × perte) = 0,62 × 7,50 – 0,38 × 5 = 4,65 – 1,90 = 2,75 euros positifs. C’est un trade à faire.”

Et boom. La décision n’est plus basée sur les sentiments. C’est basé sur les mathématiques.​

Money Management – La Vraie Différence Entre les Gagnants et les Perdants

C’est ici que la majorité des traders se trompent fondamentalement. Ils obtiennent les données Monte Carlo, ils voient une probabilité de 62%, et ensuite, ils mettent TOUS leurs euros sur ce trade unique.

C’est une catastrophe. Voici comment les vrais professionnels gèrent l’argent :​

• Si probabilité > 70% et ratio > 2:1 → Risquez 2% de votre capital total
• Si probabilité 60-70% et ratio 1,5-2:1 → Risquez 1% de votre capital
• Si probabilité 55-60% et ratio 1-1,5:1 → Risquez 0,5% de votre capital
• Si probabilité < 50% → N’effectuez pas le trade​

Pourquoi cette stratégie fonctionne-t-elle ? Parce que même les modèles statistiques les meilleur se trompent parfois. Si vous mettez 100% de votre argent sur un trade avec 62% de chances de succès, vous avez 38% de chances de perdre 100% de votre argent instantanément.​

Mais si vous risquez 1% et que vous effectuez 1 000 trades avec 62% de succès et 1,5:1 de ratio, les mathématiques garantissent que vous gagnez de l’argent à long terme. C’est mathématiquement impossible de perdre avec cette approche.​

​

Applications Avancées au-delà de la Prédiction de Prix

Monte Carlo va bien au-delà de la simple prédiction de prix d’actions individuelles :​

Construction de Portefeuille Optimisée – Vous avez 40% en actions, 30% en obligations, 30% en cash. Vous lancez Monte Carlo sur votre portefeuille entier. Vous découvrez que dans 95% des cas, vous perdrez maximum 12% cette année. Vous avez une compréhension précise de votre vrai risque avant de commencer.​

Backtesting de Stratégies – Vous avez une stratégie : “Acheter quand le prix monte trois jours de suite, vendre à la première baisse.” Vous testez cette stratégie sur 10 ans avec Monte Carlo. Vous découvrez que ça gagne 35% par an en moyenne. Mais vous découvrez aussi un drawdown maximal de 40%. Vous savez maintenant que vous devrez supporter parfois des pertes de 40% avant de revenir au succès. Vous êtes préparé mentalement.​

Stress Testing – Et si la volatilité doublait ? Et si nous avions un nouveau crash de 2008 ? Et si les taux d’intérêt montaient de 3% ? Vous testez tous ces scénarios avec Monte Carlo pour comprendre comment votre portefeuille se comporterait. Les vrais traders pro font cela quotidiennement.​

Chapitre 5 : Les Limitations Critiques que Vous Devez Connaître

L’Hypothèse de Normalité – Le Plus Grand Mensonge des Mathématiques Financières

Le modèle suppose que les rendements suivent une distribution normale, une courbe en cloche classique. Mais la réalité est bien plus brutale. Les crashes extrêmes arrivent bien plus souvent que le modèle ne le prédit.​

Les statisticiens appellent cela les “queues épaisses” – des événements extrêmes qui sont statistiquement plus probables que ne le suggère une distribution normale classique. En 2008, le modèle prédisait que le crash était un événement ayant 1 chance sur 10 000 années. Et pourtant, ça s’est passé. En 2020, le COVID a causé le plus grand crash en une semaine depuis la Grande Dépression. Les modèles disaient que c’était impossiblele.​

Nassim Taleb a écrit un livre entier, “The Black Swan”, pour critiquer précisément ce point. Monte Carlo peut significativement sous-estimer le risque réel pendant les crises.​

Paramètres Stationnaires – Une Hypothèse Fallacieuse

Le modèle suppose que la volatilité (σ) et le rendement moyen (μ) restent constants. Mais ils ne le restent jamais.​

Lors d’une crise, la volatilité peut tripler en une journée. Les rendements moyens changent radicalement de régime. Avant la crise financière, tout le monde gagnait de l’argent. Pendant la crise, tout le monde en perdait. Le modèle n’adresse pas ces changements de régime.​

Indépendance des Stocks – Une Simplification Dangereuse

Le modèle simule chaque action indépendamment. Mais en réalité, tout est corrélé.​

Lors d’un vrai crash du S&P 500, vous pensez que quelques actions vont monter pendant que d’autres baissent pour équilibrer ? Absolument pas. Elles baissent presque toutes ensemble. La corrélation se rapproche de 1, ce qui veut dire qu’elles se déplacent en tandem. Monte Carlo ne capture pas cette dynamique de corrélation écrasante lors des crises.​

Les Événements Cygne Noir – L’Imprévisible par Définition

Monte Carlo ne peut ABSOLUMENT PAS prédire les événements rares et extrêmes qui n’ont jamais eu précédent.​

Une déclaration de guerre surprise. Une faillite soudaine. Une pandémie mondiale. Un coup d’État élection. Ces choses arrivent sans prévenir, et aucun modèle statistique classique ne peut les voir venir si elles ne se sont jamais produites avant.​

C’est l’une des critiques les plus valables du système. Mais c’est aussi pourquoi les vrais professionnels combinent Monte Carlo avec d’autres approches de gestion des risques et reste attentifs aux signaux d’alerte géopolitiques.​

Conclusion : De la Théorie à la Maîtrise des Marchés

Monte Carlo, c’est une méthode statistique pour générer des milliers de scénarios basés sur les données historiques et la volatilité observée.​

Le mouvement brownien géométrique, c’est la formule mathématique sous-jacente qui rend Monte Carlo possible.​

Combinés ensemble, ils transforment le trading de “j’espère que ça marche” en “je sais que ça fonctionne en moyenne”.​

Les données actuelles du CAC 40 surpassent le S&P 500 en termes de probabilité de gain et de ratio risque-récompense.​

L’application stricte du money management – risquer seulement 0,5% à 2% par trade selon les probabilités – transforme ces modèles en générateurs de richesse fiables à long terme.​

Et maintenant que vous savez cela, vous n’avez plus d’excuses pour trader à l’aveugle. Les outils sont à votre disposition. Les mathématiques sont impitoyables. Utilisez-les.

Ce que Vous Obtiendrez en Rejoignant La Newsletter Exclusive

✓ Le Code Python Complet et Commenté – Plus de 500 lignes de code professionnel, structuré étape par étape, que vous pouvez utiliser immédiatement. Pas besoin d’être un expert en programmation. Chaque ligne est expliquée en français clair.

✓ Guide d’Installation Détaillé – Instructions précises pour installer Python, configurer les bibliothèques nécessaires (NumPy, Pandas, Matplotlib), et exécuter votre première simulation en moins de 5 minutes.

✓ Paramètres Pré-configurés – Le code arrive avec les paramètres optimisés pour les marchés français et américains actuels. Prêt à générer des résultats immédiatement.

✓ Explications Ligne par Ligne – Document détaillé expliquant chaque fonction, chaque boucle, chaque calcul probabiliste.

✓ Exemples Pratiques Avec Vraies Données – Simulations exécutées sur Tesla, Apple, Amazon, Total, Sanofi, et d’autres giants du marché.