Dans l’écosystème financier contemporain, deux révolutions technologiques majeures ont transformé radicalement les approches d’investissement et de gestion des risques : la simulation de Monte-Carlo et le trading quantitatif. Ces deux domaines, bien que distincts dans leurs origines, convergent aujourd’hui pour créer une alliance stratégique puissante, offrant aux professionnels de la finance des outils sophistiqués pour naviguer dans la complexité croissante des marchés financiers mondiaux.

Cette convergence représente un véritable tournant paradigmatique dans la finance moderne, combinant la puissance probabiliste de Monte-Carlo avec l’automatisation intelligente du trading algorithmique pour créer des stratégies d’investissement plus robustes, plus efficaces et mieux adaptées aux défis du XXIe siècle.

Monte-Carlo : Le Socle Probabiliste de la Finance Quantitative

Fondements Révolutionnaires et Applications Modernes

La simulation de Monte-Carlo, héritée des recherches scientifiques du XXe siècle, s’impose aujourd’hui comme l’épine dorsale analytique de la finance quantitative moderne. Cette méthode stochastique révolutionnaire exploite la puissance de l’aléatoire pour résoudre des problèmes financiers d’une complexité inégalée, transformant l’incertitude en données analysables et exploitables.

L’importance croissante de Monte-Carlo en finance s’explique par sa flexibilité exceptionnelle pour modéliser des instruments complexes et sa capacité unique à surmonter la malédiction de la dimensionnalité1. Cette technique permet aux analystes et investisseurs de calculer le risque et de quantifier l’impact des situations défavorables sur les plans d’investissement, offrant une vue d’ensemble prospective essentielle pour la planification stratégique.

Innovation Terminologique et Conceptuelle Révolutionnaire

Le nom “Monte-Carlo” fut choisi par Nicholas Metropolis en 1947 en référence au célèbre quartier de Monaco réputé pour ses casinos et ses jeux de hasard . Cette appellation souligne l’essence stochastique de la méthode, qui repose sur la génération de nombres aléatoires et l’échantillonnage statistique répétitif . La première publication officielle de cette méthode révolutionnaire apparaît en 1949 dans un article co-écrit par Metropolis et Ulam .

L’analogie avec les jeux de casino n’est pas fortuite : tout comme un joueur répète inlassablement ses mises pour observer la distribution des gains et pertes, la simulation de Monte-Carlo répète des milliers ou millions de scénarios aléatoires pour estimer des probabilités et des valeurs espérées dans des systèmes complexes .

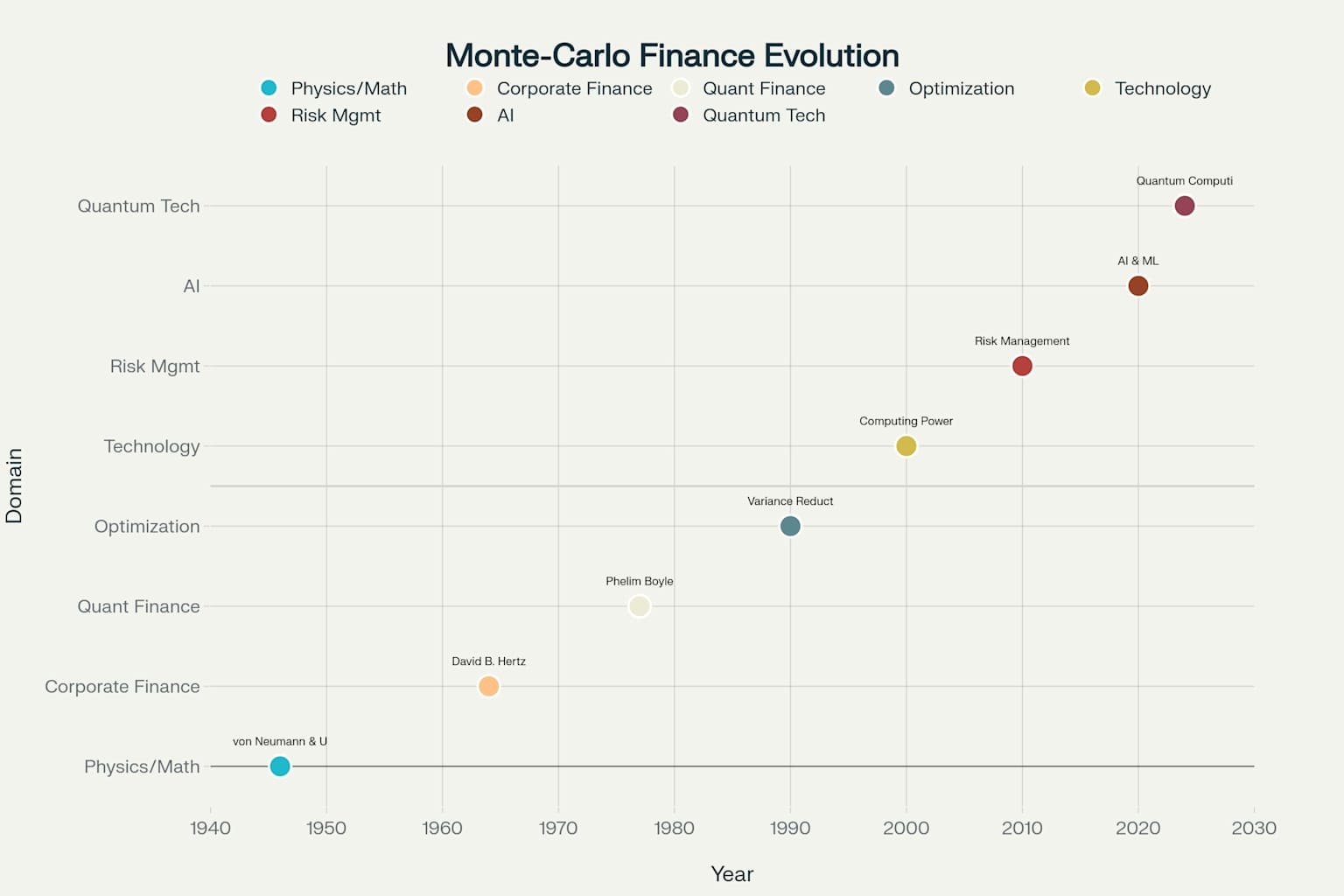
Cadre Conceptuel et Principes Fondamentaux

La simulation de Monte-Carlo repose sur un cadre théorique rigoureux ancré dans la théorie des probabilités, la statistique mathématique et l’analyse stochastique . Le principe fondamental consiste à transformer un problème déterministe en un problème probabiliste en reformulant l’estimation recherchée comme une espérance mathématique .

Mathématiquement, la méthode vise à estimer l’espérance d’une variable aléatoire X, notée E[X] . 

L’estimateur de Monte-Carlo ou estimateur de la moyenne empirique s’exprime par la formule μₙ := (1/n)∑ᵢ₌₁ⁿ Xᵢ, où X₁, X₂, …, Xₙ sont des variables aléatoires indépendantes et identiquement distribuées (iid) suivant la même loi que X .

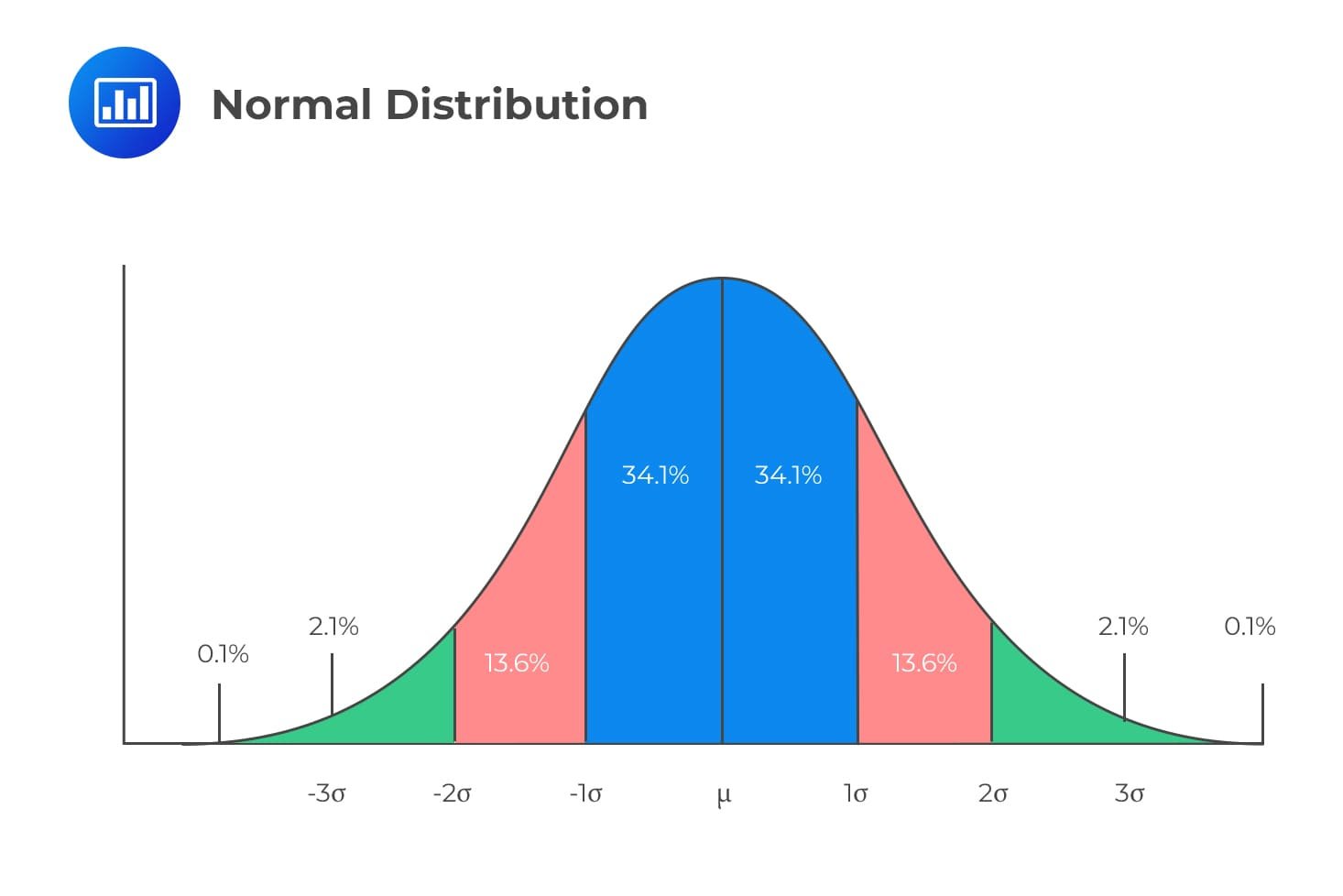
Illustration of a normal distribution, showing the percentage of data falling within each standard deviation from the mean analystprep

Trading Quantitatif : L’Automatisation Intelligente des Décisions

Évaluation et Pricing des Instruments Dérivés Complexes

La simulation de Monte-Carlo excelle dans l’évaluation des options et autres instruments dérivés complexes, particulièrement lorsque les formules analytiques fermées sont inexistantes ou impraticables . 

Pour une option d’achat européenne, le processus de Monte-Carlo suit une méthodologie rigoureuse incluant la simulation de trajectoires, le calcul des payoffs, l’actualisation et l’estimation du prix .

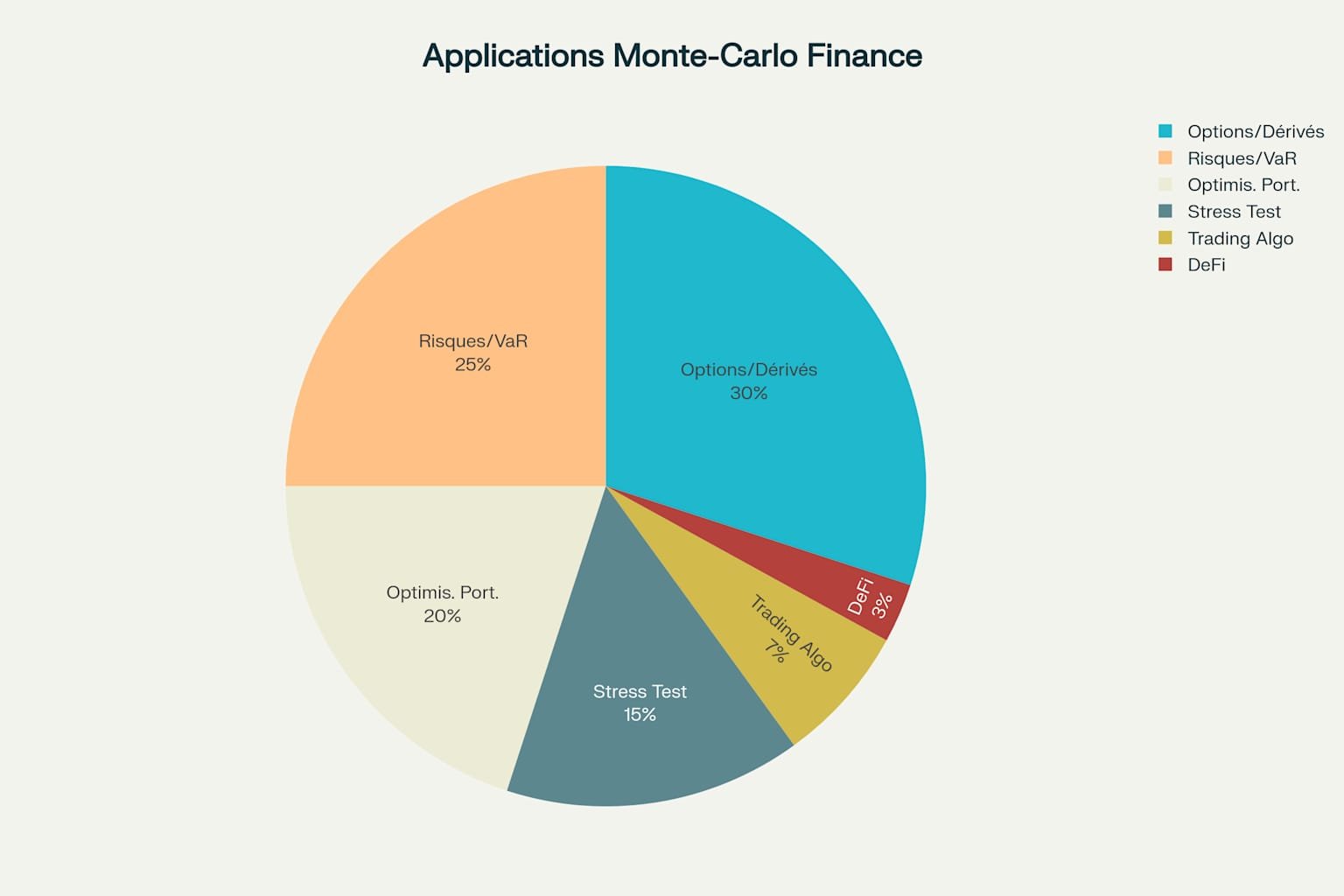
Répartition des applications de Monte-Carlo en finance moderne par domaine d’utilisation

La véritable puissance de Monte-Carlo se révèle dans l’évaluation d’options exotiques dont la valeur dépend de l’évolution complète du prix de l’actif sous-jacent . Les options asiatiques utilisent la moyenne arithmétique ou géométrique des prix observés sur une période donnée, tandis que les options à barrière intègrent des barrières activantes ou désactivantes . Pour les produits de crédit com

Stratégies Fondamentales et Méthodes Avancées

Les stratégies de trading quantitatif englobent plusieurs approches sophistiquées : l’arbitrage statistique qui recherche des relations statistiques entre différents actifs, les stratégies de momentum et mean reversion qui exploitent les patterns temporels, et le market making qui profite des spreads bid-ask. Ces stratégies reposent sur des règles prédéfinies et des algorithmes automatisés qui éliminent les biais emotionnels.

Le processus de développement suit une méthodologie rigoureuse incluant l’analyse des données historiques, la création de modèles basés sur des règles, le backtesting extensif, et l’optimisation continue. Cette approche systématique garantit la reproductibilité et la scalabilité des performances.

L’Alliance Stratégique : Convergence et Synergie

Intégration Technologique et Optimisation Multi-Objectifs

La convergence entre Monte-Carlo et trading quantitatif crée une synergie technologique puissante qui démultiplie les capacités analytiques et décisionnelles. Monte-Carlo apporte sa capacité à modéliser l’incertitude et à générer des distributions complètes de résultats, tandis que le trading quantitatif offre ses algorithmes d’optimisation et d’exécution automatisée.

Cette intégration permet l’optimisation multi-objectifs des portefeuilles en utilisant des algorithmes génétiques combinés aux simulations Monte-Carlo. Les trajectoires probables des actifs financiers sont projetées stochastiquement, permettant de définir plusieurs indices de qualité par trajectoire et d’optimiser l’allocation selon différents critères potentiellement contradictoires.

Applications Avancées et Gestion des Risques

L’alliance stratégique se manifeste particulièrement dans la gestion des risques avancée, où Monte-Carlo génère des scénarios multiples pour le calcul de la Value at Risk (VaR) et du Conditional Value at Risk (CVaR), tandis que les algorithmes quantitatifs automatisent les ajustements de portefeuille en temps réel. Cette approche permet une gestion dynamique et proactive des expositions aux risques.

Les applications incluent également l’évaluation d’options complexes où Monte-Carlo simule les trajectoires de prix et calcule les payoffs, tandis que les systèmes de trading quantitatif optimisent les stratégies de couverture et d’arbitrage. Cette combinaison permet de traiter des instruments financiers d’une complexité sans précédent.

Techniques Avancées et Optimisation Computationnelle

Réduction de Variance et Efficacité Algorithmique

L’optimisation de l’alliance Monte-Carlo/trading quantitatif passe par l’implémentation de techniques de réduction de variance sophistiquées3. Les variables antithétiques permettent de générer des paires de chemins corrélés négativement, réduisant significativement la variance des estimations tout en diminuant le coût computationnel3.

Les méthodes quasi-Monte-Carlo, utilisant des séquences à faible discrépance comme les séquences de Sobol, offrent une vitesse de convergence supérieure O(1/N) versus O(N⁻⁰·⁵) pour Monte-Carlo classique3. Cette amélioration est cruciale pour les applications de trading haute fréquence nécessitant des calculs en temps réel.

Intelligence Artificielle et Apprentissage Automatique

L’intégration de l’intelligence artificielle révolutionne l’alliance stratégique en permettant aux algorithmes d’apprendre des patterns complexes dans les données financières. Les réseaux de neurones peuvent approximer les fonctions de payoff complexes, réduisant considérablement le temps de calcul des simulations Monte-Carlo.

L’approche Neural Monte-Carlo utilise des réseaux de neurones profonds pour améliorer la qualité des simulations, tandis que les systèmes d’IA analysent en temps réel de vastes quantités de données pour optimiser les stratégies de trading. Cette convergence crée des systèmes adaptatifs capables d’évoluer avec les conditions de marché.

Backtesting et Validation : L’Excellence Méthodologique

Protocoles de Validation Rigoureux

Le backtesting constitue la pierre angulaire de la validation des stratégies combinant Monte-Carlo et trading quantitatif. Cette étape cruciale permet d’évaluer la performance historique des stratégies tout en identifiant les paramètres optimaux et les profils de risque.

Les meilleures pratiques incluent la division train-test, la validation croisée, l’analyse walk-forward, et la simulation Monte-Carlo des résultats de backtesting. Cette approche multi-niveaux garantit la robustesse des stratégies et réduit les risques de suroptimisation.

Métriques de Performance et Analyse des Risques

La simulation de Monte-Carlo constitue un pilier fondamental de la gestion moderne des risques financiers, offrant une approche sophistiquée pour quantifier et analyser les expositions aux risques dans des portefeuilles complexes . La Value at Risk (VaR) représente la perte potentielle maximale qu’un portefeuille peut subir sur une période donnée avec un niveau de confiance spécifié .

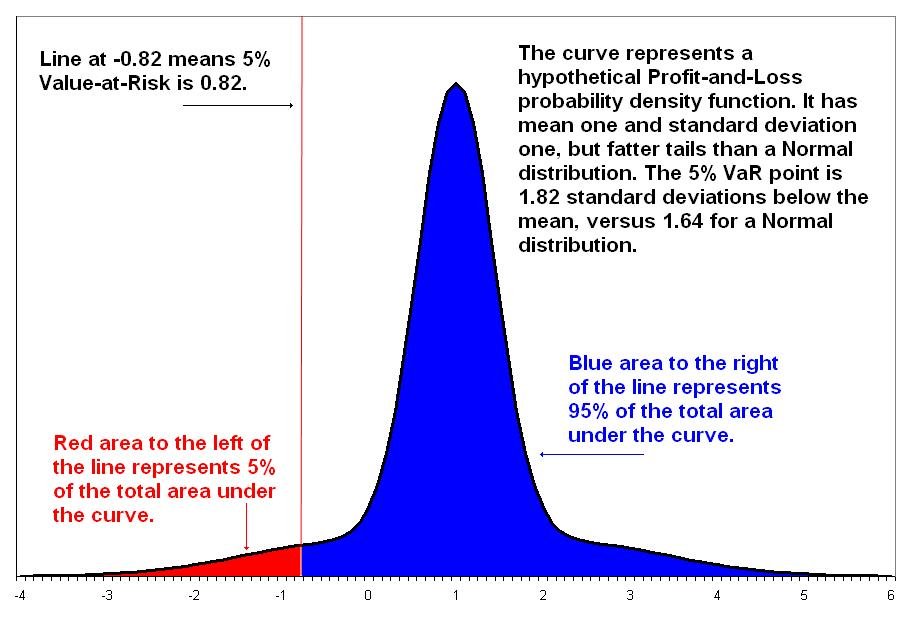
A probability density function illustrating the 5% Value-at-Risk (VaR) point, with the red area representing the worst 5% of outcomes wikipedia

Le processus méthodologique de calcul de la VaR par Monte-Carlo inclut la modélisation des facteurs de risque, la génération de scénarios, la valorisation du portefeuille et l’analyse statistique . Monte-Carlo permet également de réaliser des tests de résistance sophistiqués en simulant

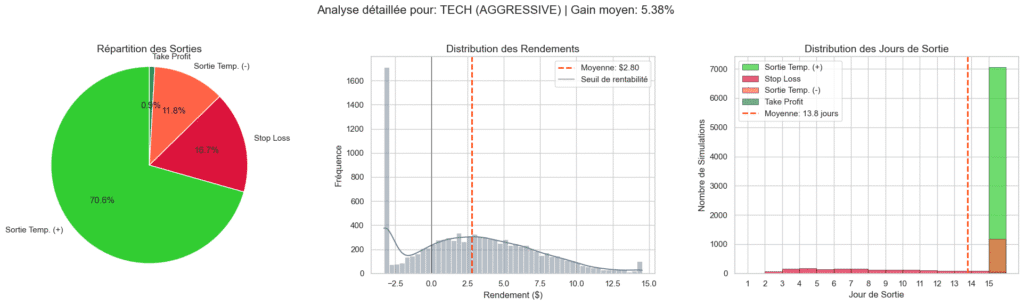
Exemple de résultats d’analyse de risque grâce à Monte-Carlo

Application moderne

L’application de Monte-Carlo à l’optimisation de portefeuille révolutionne l’approche traditionnelle de Markowitz en introduisant une perspective forward-looking basée sur des simulations probabilistes . La simulation Monte-Carlo permet de générer des milliers de combinaisons de portefeuilles avec des poids aléatoires, puis d’analyser leurs caractéristiques risque-rendement pour identifier la frontière efficiente optimale .

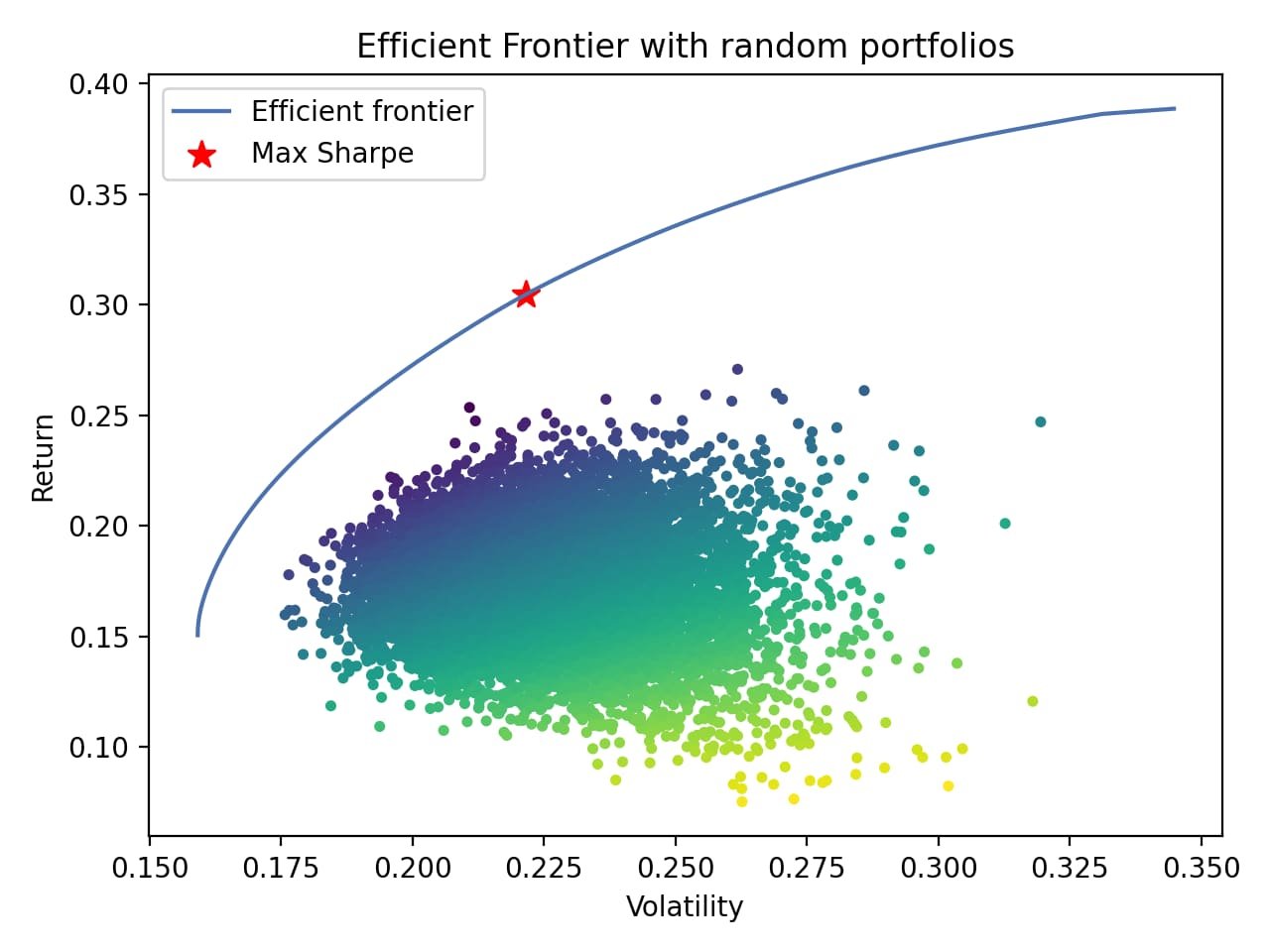
Efficient frontier plot showing random portfolios with risk (volatility) versus return, highlighting the maximum Sharpe ratio portfolio readthedocs

Le processus d’optimisation par Monte-Carlo inclut la génération de poids aléatoires, le calcul des métriques, l’identification de l’optimum et l’analyse de sensibilité . Les approches ESG utilisent Monte-Carlo pour intégrer les critères environnementaux, sociaux et de gouvernance dans l’optimisation, avec des portefeuilles dont le degré ESG est calculé en sommant les produits des poids d’actifs et des scores ESG .

Cet article est un cross-post exclusif avec ma newsletter “Algo & Backtest”. Si tu veux aller plus loin, je t’invite à t’abonner : dans la dernière édition, je détaille tous les aspects techniques abordés ici, et je mets à disposition un code Python prêt à l’emploi pour réaliser tes propres analyses Monte-Carlo et backtests quantitatifs.

👉 Découvre la newsletter ici : [LIEN VERS LA NEWSLETTER]

Perspectives d’Avenir et Innovations Émergentes

Calcul Quantique et Révolution Computationnelle

L’avenir de l’alliance Monte-Carlo/trading quantitatif s’annonce révolutionnaire avec l’émergence du calcul quantique. Les ordinateurs quantiques promettent de résoudre des équations aux dérivées partielles en haute dimension avec une complexité polynomiale plutôt qu’exponentielle, transformant l’évaluation d’instruments ultra-complexes.

Cette avancée permettra des simulations en temps réel de portefeuilles massifs et l’optimisation simultanée de milliers de stratégies de trading, ouvrant des perspectives inédites pour la finance quantitative.

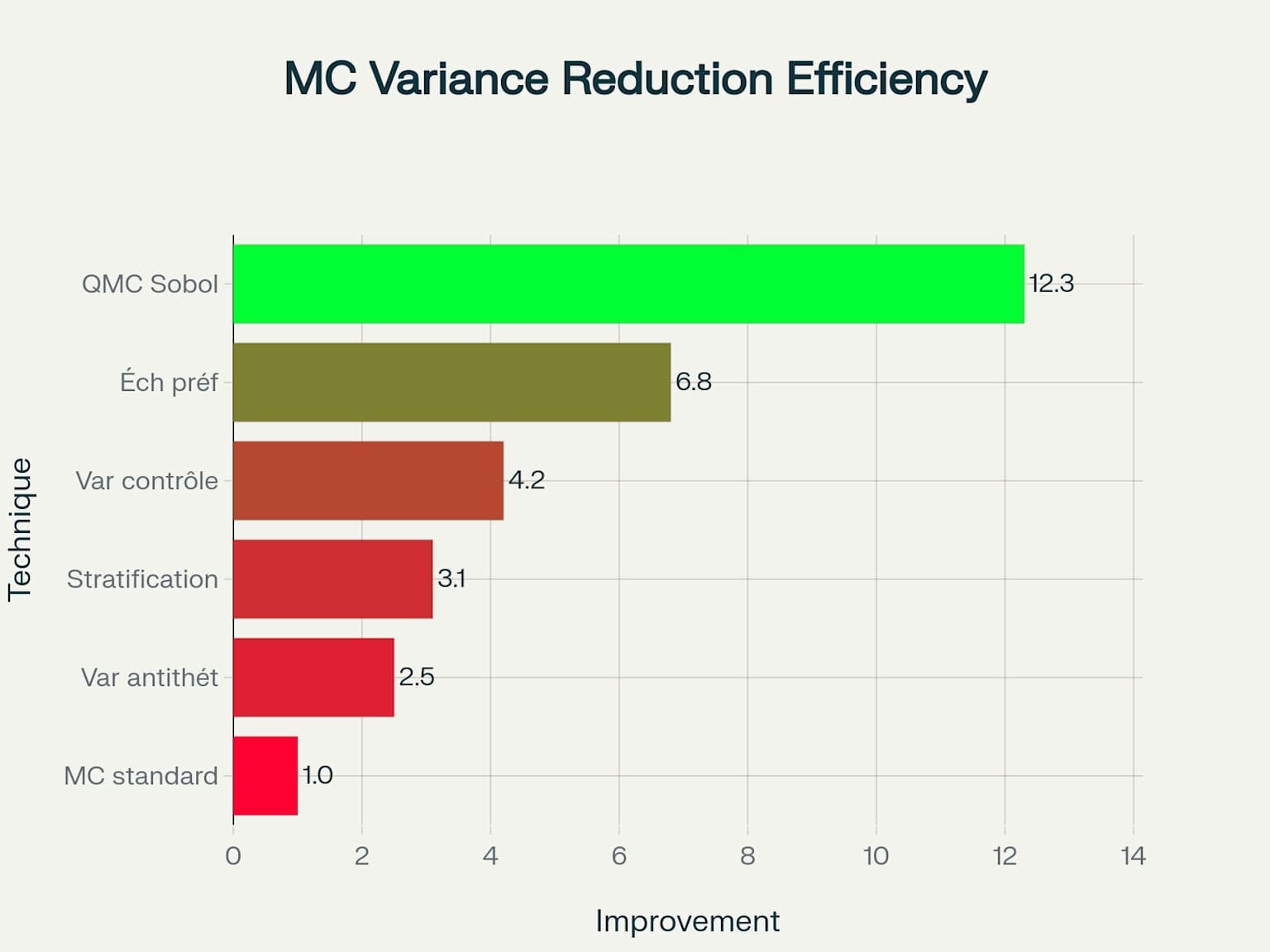
Comparaison de l’efficacité des techniques de réduction de variance en Monte-Carlo

Finance Durable et Modélisation ESG

L’adaptation aux enjeux de la finance durable représente un défi majeur pour l’alliance stratégique3. Monte-Carlo s’adapte pour modéliser les risques climatiques et les transitions énergétiques, tandis que les algorithmes quantitatifs intègrent les critères ESG dans l’optimisation de portefeuilles.

Les stress tests climatiques utilisent Monte-Carlo pour simuler des scénarios de réchauffement sur 30 ans, évaluant l’impact sur les modèles d’affaires et les valorisations financières. Cette évolution positionne l’alliance au cœur des enjeux sociétaux contemporains.

Conclusion : L’Excellence Quantitative au Service de la Performance

L’alliance stratégique entre la simulation de Monte-Carlo et le trading quantitatif représente un paradigme révolutionnaire de la finance moderne, combinant la rigueur mathématique avec l’innovation technologique pour créer des solutions d’investissement d’une sophistication inégalée.

Cette convergence offre aux professionnels de la finance des outils exceptionnellement puissants pour naviguer dans l’incertitude, optimiser les performances, et gérer les risques de manière proactive. La synergie entre la modélisation probabiliste de Monte-Carlo et l’automatisation intelligente du trading quantitatif crée des opportunités d’alpha génération et d’optimisation de portefeuille sans précédent.

L’avenir de cette alliance s’annonce particulièrement prometteur avec l’intégration du calcul quantique, de l’intelligence artificielle avancée, et des enjeux de durabilité. Ces évolutions technologiques et sociétales promettent de décupler la puissance analytique tout en répondant aux défis contemporains de la finance responsable.

Pour maximiser l’efficacité de cette alliance stratégique, les organisations financières doivent investir dans une infrastructure technologique robuste, développer les compétences quantitatives de leurs équipes, et maintenir une approche rigoureuse de validation et de gestion des risques. L’excellence dans cette alliance représente un avantage concurrentiel décisif dans l’environnement financier de plus en plus complexe et interconnecté du XXIe siècle.

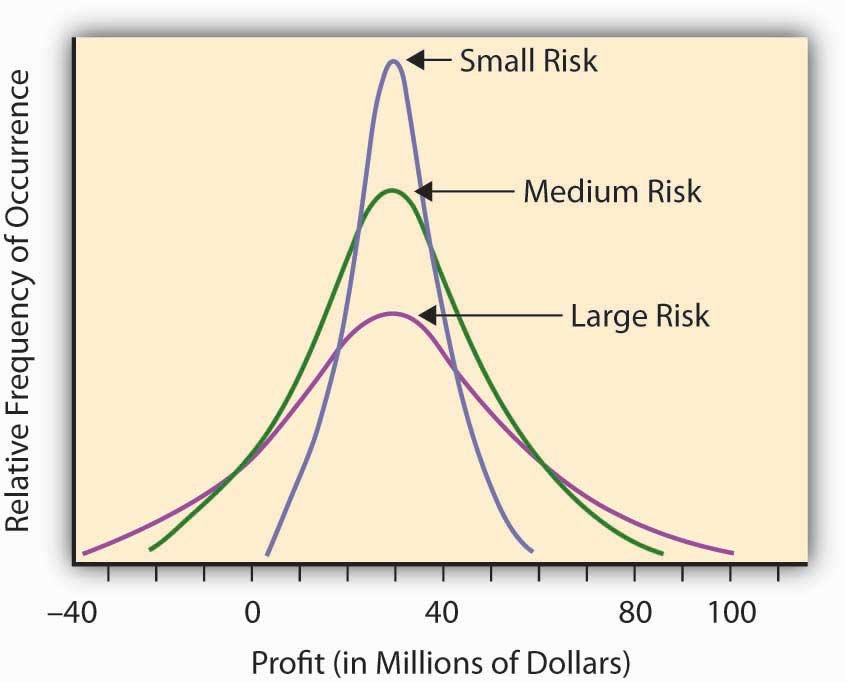
Profit distribution curves illustrating varying levels of financial risk based on the spread of potential outcomes github